원본 playtechs.blogspot.com/2007/04/aiming-at-moving-target.html
Aiming a projectile at a moving target
To hit a moving target by shooting a gun you have to lead it, aiming at the spot where the target will be when the bullet reaches it. In t...
playtechs.blogspot.com

To hit a moving target by shooting a gun you have to lead it, aiming at the spot where the target will be when the bullet reaches it. In this article we consider three successively harder versions of this problem.
총을 쏘아 움직이는 목표물을 맞추려면 총알이 닿았을 때 목표물이있을 지점을 겨냥하여 이끌어야합니다. 이 기사에서 우리는이 문제의 세 가지 연속적으로 어려운 버전을 고려합니다.
To simplify the math, express the target's position and velocity relative to the shooter's, so that the shooter is effectively stationary at the origin. Assume that the target moves in a straight line, if it is moving. Also assume no air drag.
수학을 단순화하려면 사수가 원점에 효과적으로 고정되도록 목표의 위치와 사수의 상대적인 속도를 표현합니다. 목표물이 움직이면 직선으로 움직인다고 가정합니다. 또한 공기 저항이 없다고 가정합니다.
Motion without gravity
Without gravity, bullets travel in a straight line at constant velocity. To determine where to shoot, imagine shooting an infinite number of bullets simultaneously in all directions, forming an expanding sphere of death. While the sphere is expanding, the target is moving along a straight line (or standing still). If we can determine the instant at which this expanding sphere touches the moving target, we know where to aim: at the target's position when it gets hit by the expanding sphere of death.
중력이 없으면 총알은 일정한 속도로 직선으로 이동합니다. 사격 할 곳을 결정하기 위해 모든 방향으로 무한한 수의 총알을 동시에 쏘아서 확장되는 죽음의 영역을 형성한다고 상상해보십시오. 구가 확장되는 동안 대상은 직선을 따라 이동하거나 가만히 서 있습니다. 이 팽창하는 구체가 움직이는 표적에 닿는 순간을 결정할 수 있다면, 우리는 어디를 조준해야할지 알 수 있습니다. 팽창하는 죽음의 구체에 맞았을 때 표적의 위치를 겨냥합니다.
Variable definitions:

Equation for the time when the target and bullet are equidistant from the shooter:
목표물과 총알이 사수로부터 등거리에있을 때의 방정식 :
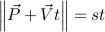
Square both sides: 양쪽 정사각형 :
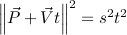
Expand: 넓히다:
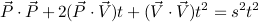
Group terms by powers of t: t의 거듭 제곱으로 용어 그룹화 :
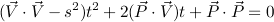
Examine the equation above. If the target's velocity is zero, the impact time works out to simply be target distance divided by bullet speed, which makes sense. The constant term is never negative; it is positive as long as shooter and target are not at the same position. The quadratic term curves upward if the target's speed is faster than the bullet speed. In this case, only the linear term would be capable of bringing the curve below the zero line. In problem terms: if the target is faster than the bullet, the bullet can hit the target only if the target is moving toward the shooter fast enough.
위의 방정식을 살펴보십시오. 목표의 속도가 0이면 충돌 시간은 단순히 목표 거리를 총알 속도로 나눈 값으로 계산됩니다. 상수항은 절대 음수가 아닙니다. 사수와 표적이 같은 위치에 있지 않는 한 긍정적입니다. 목표의 속도가 총알 속도보다 빠르면 2 차 항은 위쪽으로 구부러집니다. 이 경우 선형 항만 곡선을 0 선 아래로 가져올 수 있습니다. 문제의 경우 : 목표물이 총알보다 빠르면 목표물이 사수쪽으로 충분히 빠르게 이동하는 경우에만 총알이 목표물을 맞출 수 있습니다.
Code for solving this quadratic might look like this: 이 2 차를 풀기위한 코드는 다음과 같습니다.
double time_of_impact(double px, double py, double vx, double vy, double s)
{
double a = s * s - (vx * vx + vy * vy);
double b = px * vx + py * vy;
double c = px * px + py * py;
double d = b*b + a*c;
double t = 0;
if (d >= 0)
{
t = (b + sqrt(d)) / a;
if (t < 0)
t = 0;
}
return t;
}I've done a bit more simplification in going from the equation to the code. Any time there's a 2 on the linear coefficient of the quadratic (which actually happens fairly frequently in my experience), it cancels with the 2 in the denominator and the 4 in the discriminant of the usual quadratic formula. Also, negating the quadratic coefficient (a in the code) cleans out a few minus signs.
방정식에서 코드로 이동하는 과정에서 좀 더 단순화했습니다. 2 차의 선형 계수에 2가있을 때 (실제로 내 경험상 꽤 자주 발생 함), 분모에 2가 있고 일반적인 2 차 공식의 판별에 4가 있으면 취소됩니다. 또한 2 차 계수 (코드에서 a)를 부정하면 몇 개의 마이너스 기호가 제거됩니다.
Once t is known, plug it into the expression for the motion of the target to find the point to aim at:
t를 알고 나면 목표물의 움직임에 대한 표현식에 연결하여 조준 할 지점을 찾습니다.
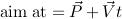
This code works equally well with 3D vectors. In a real game I'd be using a vector data type rather than passing around the X, Y, and Z components individually, and I'd have a function for doing dot products instead of writing out x1*x2 + y1*y2 + z1*z2 every time.
이 코드는 3D 벡터에서도 똑같이 잘 작동합니다. 실제 게임에서는 X, Y, Z 구성 요소를 개별적으로 전달하는 대신 벡터 데이터 유형을 사용하고 x1 * x2 + y1 * y2 +를 쓰는 대신 내적을 수행하는 함수를 사용합니다. 매번 z1 * z2.
If the discriminant (d in the code) is less than zero, it means there are no real roots. In real terms this means the target is moving away faster than the bullet can travel, so there is no possibility of an impact. The code deals with the no-root situation by clamping t to zero, which will cause the gun to aim at the target's current position. A more sensible thing to do might be to find the time t that minimizes distance between bullet and target, and aim at the target's position then.
판별 자 (코드에서 d)가 0보다 작 으면 실제 근이 없음을 의미합니다. 실제적으로 이것은 목표물이 총알이 이동할 수있는 것보다 빨리 멀어 지므로 충격의 가능성이 없음을 의미합니다. 이 코드는 t를 0으로 고정하여 루트가없는 상황을 처리합니다. 그러면 총이 표적의 현재 위치를 조준합니다. 더 현명한 방법은 총알과 표적 사이의 거리를 최소화하는 시간 t를 찾아 표적의 위치를 조준하는 것입니다.
There is also generally a negative root which corresponds to playing time backwards from the current moment, and as such is not usable.
또한 일반적으로 현재 순간에서 뒤로 재생 시간에 해당하는 음의 루트가 있으므로 사용할 수 없습니다.
Space combat games such as Freelancer or Darkstar One draw a targeting reticle ahead of enemy ships, at the spot where you need to shoot in order to hit them. Now you can go forth and do likewise. Obviously, the aim position is different for different bullet speeds, so if you have turbolasers that shoot at 4.5 km/sec and linear tachyon atomizers that shoot at 6 km/sec, you might want two reticles.
Freelancer 또는 Darkstar One과 같은 우주 전투 게임은 적 군함을 공격하기 위해 촬영해야하는 지점에서 적 군함 앞에 조준 십자선을 그립니다. 이제 당신은 나아가서 그렇게 할 수 있습니다. 분명히 목표 위치는 총알 속도에 따라 다르므로 4.5km / sec로 발사하는 터보 레이저와 6km / sec로 발사하는 선형 타키온 분무기가 있다면 두 개의 레티클이 필요할 수 있습니다.
Gravity without motion
On earth, gravity pulls bullets downward as they fly. (They also slow down quite a bit due to air resistance, but I'm not going to get into that today.) To counteract gravity you have to aim higher for far-away targets. Let's figure out how to do this with a stationary target first.
지구상에서 중력은 총알이 날아갈 때 아래쪽으로 당깁니다. (그들은 또한 공기 저항으로 인해 상당히 느려지지만 오늘은 그것에 대해 다루지 않을 것입니다.) 중력에 대항하려면 멀리있는 목표물을 더 높게 조준해야합니다. 먼저 고정 타겟으로이 작업을 수행하는 방법을 알아 봅시다.
Returning to our expanding sphere of death, we could imagine it falling due to gravity as it expands. Equivalently, we could think of the stationary target “falling” upward into the sky instead. This allows us to leave the sphere centered on the origin. Here's the equation for a target which starts at rest and falls upward until it hits the expanding sphere:
팽창하는 죽음의 영역으로 돌아가서, 우리는 그것이 팽창함에 따라 중력으로 인해 떨어지는 것을 상상할 수 있습니다. 마찬가지로, 우리는 고정 된 목표물이 대신 하늘 위로 "떨어지는"것을 생각할 수 있습니다. 이것은 우리가 원점의 중심에 구를 떠날 수있게합니다. 다음은 정지 상태에서 시작하여 확장하는 구체에 도달 할 때까지 위쪽으로 떨어지는 대상에 대한 방정식입니다.
In a typical game, gravity operates along a single axis. In this case, the G vector will have zeros in all the other components. Squaring:
일반적인 게임에서 중력은 단일 축을 따라 작동합니다. 이 경우 G 벡터는 다른 모든 구성 요소에서 0을 갖습니다. 제곱 :
Expand:
Group terms by power of t:
Although we have a fourth power of t, we can substitute u = t2 and be left with a quadratic instead:
t의 4 제곱이 있지만 u = t2로 대체하고 대신 2 차로 남길 수 있습니다.
The two solutions to this u quadratic correspond to the two parabolic arcs that pass through the target point. There's a short, low arc and a longer, high arc. (At maximum range they merge together into one.) Choose whichever one works best for your situation.
이 u 2 차에 대한 두 솔루션은 목표점을 통과하는 두 포물선 호에 해당합니다. 짧고 낮은 호와 더 길고 높은 호가 있습니다. (최대 범위에서는 하나로 합쳐집니다.) 상황에 가장 적합한 것을 선택하십시오.
Once you've solved for t, plug it into the equation for motion of the target to get the aim position:
t에 대해 풀었 으면 목표 위치를 얻기 위해 대상의 움직임에 대한 방정식에 연결합니다.
Be sure that your targeting code integrates to the same position your simulation will when it moves the bullet through the air. The equations above assume correct integration, but as a kid I wrote things that weren't quite right. For instance:
표적 코드가 총알을 공중으로 이동할 때 시뮬레이션과 동일한 위치에 통합되어야합니다. 위의 방정식은 올바른 통합을 가정하지만 어렸을 때 옳지 않은 것을 썼습니다. 예를 들면 :
newPosition = oldPosition + oldVelocity;
newVelocity = oldVelocity + acceleration;
The code is assuming that velocity is expressed in distance per frame, and acceleration in distance per frame squared. However, it should be adding half the acceleration to the position as well, like this:
이 코드는 속도가 프레임 당 거리로 표현되고 가속도는 프레임 당 거리로 제곱된다고 가정합니다. 그러나 다음과 같이 위치에 가속도의 절반도 추가해야합니다.
newPosition = oldPosition + oldVelocity + 0.5 * acceleration;
newVelocity = oldVelocity + acceleration;
Gravity and motion together
Finally, let's shoot an arcing projectile at a moving target! The initial equation is just a combination of the starting equations for the previous two cases:
마지막으로 움직이는 목표물에 아크 발사체를 쏘자! 초기 방정식은 앞의 두 경우에 대한 시작 방정식의 조합 일뿐입니다.
Square:
Expand:
Collect terms by power of t:
This is a quartic equation and there's no way around it. Let's start by sanity-checking it.
이것은 4 차 방정식이고 주위에 방법이 없습니다. 온 전성 검사부터 시작하겠습니다.
If gravity is zero, the quartic and cubic terms drop out (as well as part of the quadratic term) and we're left with the motion-but-no-gravity equation. If velocity is zero instead, the cubic and linear terms drop out (as well as part of the quadratic term) and we're left with the gravity-but-no-motion equation.
중력이 0이면 4 차항과 3 차항이 (2 차항의 일부와 함께) 빠져 나가고 우리는 운동이지만 중력이없는 방정식을 남깁니다. 대신 속도가 0이면 3 차항과 선형 항이 (2 차항의 일부와 함께) 빠져 나가고 우리는 중력이 있지만 운동이없는 방정식을 남깁니다.
When I'm working on solving problems like this, I find it helpful to rig up my game to plot graphs in real time. In this case, I drive the target around and get a constantly-updated graph of the polynomial and its derivatives for shooting at it. This allows me to quickly get a feel for the nature of the problem. Here's an example graph (with added labels):
이런 문제를 해결하기 위해 작업 할 때 실시간으로 그래프를 그릴 수 있도록 게임을 구성하는 것이 도움이됩니다. 이 경우, 나는 목표물을 돌아 다니며 계속해서 업데이트되는 다항식 그래프와 그 파생물을 얻습니다. 이를 통해 문제의 본질을 빠르게 파악할 수 있습니다. 다음은 라벨이 추가 된 그래프의 예입니다.
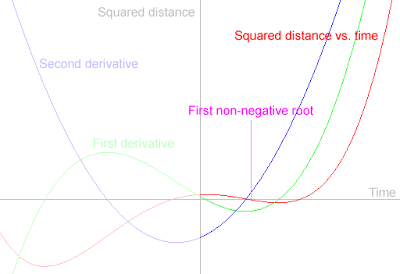
Looking at the equation, you can see that the fourth-order term will always be positive, which means that the red curve will always turn upward on the outer ends. The constant term will always be positive as long as the target is not at the same place as the shooter, which means the curve will be positive as it crosses the Y axis.
방정식을 보면 4 차 항이 항상 양수라는 것을 알 수 있습니다. 즉, 빨간색 곡선이 항상 바깥 쪽 끝에서 위쪽으로 회전한다는 것을 의미합니다. 목표가 사수와 같은 위치에 있지 않는 한 상수 항은 항상 양수입니다. 즉, 곡선이 Y 축을 가로 지르면 양수가됩니다.
The quartic curve has (up to) three points where it changes direction from upward to downward or vice versa. One way to find the roots would be to divide the curve up into intervals between these points. If one end of an interval is above zero and the other is below zero, you know there is a root within that interval. You could use a binary search to locate it, or you could use the midpoint of the interval as an initial guess and use Newton's method to converge on the root. The outer intervals are unbounded so binary search wouldn't necessarily work there, but you could double a t value until it evaluates positive and then binary search within that interval.
4 차 곡선에는 위쪽에서 아래쪽으로 또는 그 반대로 방향이 변경되는 (최대) 세 개의 점이 있습니다. 근을 찾는 한 가지 방법은 곡선을이 점 사이의 간격으로 나누는 것입니다. 간격의 한쪽 끝이 0보다 크고 다른 쪽 끝이 0보다 작 으면 해당 간격 내에 근이 있음을 알 수 있습니다. 이진 검색을 사용하여 찾을 수도 있고 간격의 중간 점을 초기 추측으로 사용하고 Newton의 방법을 사용하여 근에서 수렴 할 수 있습니다. 외부 간격은 제한이 없으므로 이진 검색이 반드시 거기에서 작동하지는 않지만 양수로 평가 될 때까지 t 값을 두 배로 계산 한 다음 해당 간격 내에서 이진 검색을 두 배로 할 수 있습니다.
The extrema of the quartic correspond to zeros (roots) of its first derivative (the green line in the graph). The first derivative of a quartic is a cubic. We could follow a similar procedure to find its roots: find the zeros of its derivative (the blue line); use them to subdivide the curve into intervals; evaluate the function at the interval endpoints; and search for roots in the intervals that cross the X axis.
4 차의 극값은 1 차 도함수 (그래프의 녹색 선)의 0 (근)에 해당합니다. 4 차의 1 차 도함수는 3 차입니다. 우리는 그 뿌리를 찾기 위해 비슷한 절차를 따를 수 있습니다 : 그것의 미분 (파란색 선)의 0을 찾습니다. 그것들을 사용하여 곡선을 간격으로 세분화하십시오. 간격 끝점에서 함수를 평가합니다. X 축을 가로 지르는 구간에서 근을 검색합니다.
When there are no roots, I decided I wanted my gun to shoot at an angle that brought the bullets as close as possible to the target. This corresponds to finding the non-negative t that gives the smallest value for the quartic function. Minima have to be either at one of the zeros of the first derivative, or at t = 0. Once the roots of the cubic are known it's simple to evaluate the function at them, and at t = 0, and pick the one with the smallest value.
뿌리가 없으면 총알이 목표물에 최대한 가깝게 맞도록 총을 쏘고 싶었습니다. 이것은 4 차 함수에 대해 가장 작은 값을 제공하는 음이 아닌 t를 찾는 것에 해당합니다. 최소값은 1 차 도함수의 0 중 하나 또는 t = 0에 있어야합니다. 3 차의 근이 알려지면 해당 함수를 간단하게 평가하고 t = 0에서 가장 작은 값.
Jochen Schwarze wrote some cubic/quartic solving code in Graphics Gems I which works great.
Jochen Schwarze는 잘 작동하는 Graphics Gems I에서 3 차 / 4 차 해석 코드를 작성했습니다.
Once again, once t is known, plug it into the left-hand side of the original equation to get the aim position:
다시 한 번 t가 알려지면 원래 방정식의 왼쪽에 연결하여 조준 위치를 얻습니다.
Ron Levine wrote a Usenet posting a few years ago covering some of the same ground. There's also a page on the Unreal Wiki.
Ron Levine은 몇 년 전에 동일한 근거를 다루는 Usenet 게시물을 작성했습니다. Unreal Wiki에도 페이지가 있습니다.
Posted by James McNeill at 8:00 AM
Labels: how-to
'Bullet Physics' 카테고리의 다른 글
| Bullet physics - dynamic world with libgdx (0) | 2021.03.25 |
|---|---|
| Bullet physics - collision world with libgdx (0) | 2021.03.25 |
| BulletQuickstart (0) | 2020.12.15 |
| Actions: Vehicles & Character Controller (0) | 2020.12.03 |
| Constraints (0) | 2020.12.03 |
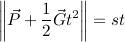
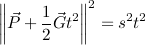
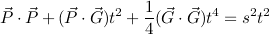
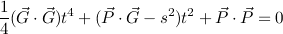
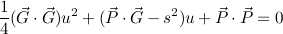
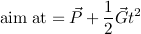
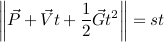
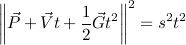
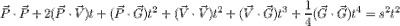
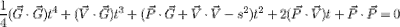
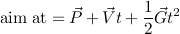


댓글